이진 탐색 트리란?
이진트리는 자식 노드가 최대 두 개인 노드들로 구성된 트리를 뜻합니다.
이진탐색 트리(Binary Search Tree)는 이진 탐색(Binary Search)와 연결 리스트(Linked list)를 결합한 이진트리입니다.
이진 탐색은 시간복잡도가 O(logN)이지만 정렬된 상태를 유지해야 함으로 삽입이나 삭제가 불가능합니다.
연결 리스트는 삽입이나 삭제시 O(1)의 상수 시간복잡도로 처리 가능하지만, 탐색 시간복잡도가 O(N)입니다.
정리하자면 이 둘의 장점을 챙긴 자료구조가 이진 탐색트리입니다.
이진 탐색 트리의 특징
- 모든 왼쪽 자식의 노드의 값이 부모 노드의 값보다 작습니다.
- 모든 오른쪽 자식의 노드의 값이 부모 노드의 값보다 큽니다.
- 각 노드들은 서로 유일한 값을 가집니다.

위 그림에서 왼쪽 트리는 BST에 속합니다. 하지만 오른 쪽 트리는 BST가 아닙니다.
값이 3인 노드를 기준으로 오른쪽에 서브트리에는 큰 값만 위치해야 되는데 3보다 작은 2가 위치해 있기 때문입니다.
이진 탐색 트리는 균형이 매우 중요합니다. 만약 이진 탐색 트리가 균형이 잡혀있지 않게 된다면,
한쪽으로 노드들이 몰리게 될 수 있습니다. 이렇게 되면 탐색할 때 시간이 더 걸리게 됨으로, 삽입과 삭제마다 트리의
구조를 재조정하는 알고리즘을 추가할 수 있습니다.
만약 처음에 데이터를 5 - 4 - 3 - 2 -1 순으로 이진 탐색 트리에 데이터를 넣게되면 다음과 같은
트리의 형태를 띌겁니다.

이진 트리가 O(logN)의 시간 복잡도를 보장하는 이유는 루트 노드를 기준으로 찾으려는 값이 큰값이면
오른쪽으로 작은 값이면 왼쪽으로 탐색을 진행하면 결론적으로 트리의 높이인 O(logN)이 나오게 되는데
만약 모든 트리가 위와 같이 왼쪽으로 몰려있게 된다면, 노드의 갯수 만큼 시간이 걸리게 됩니다. 따라서 O(n)의 시간복잡도를 가지게 됩니다. 따라서 이진 탐색 트리에 있어서 균형은 매우 중요하다고 할 수 있겠습니다.
순회방법
이진 탐색 트리는 순회할 때 중위 순회 방법을 사용합니다.
중위 순회는 [ 왼쪽 자식 - 루트 - 오른쪽 자식] 순으로 순회하는 것을 의미합니다.

예를 들어 위와 같은 이진 탐색 트리가 있을 경우 순회 순서는 다음과 같습니다.
[ 1 - 3 - 4 - 5 - 7 - 6 - 8 - 9]
순회한 결과를 보면 정렬되어 있는 것을 알 수 있습니다.
이진 탐색 트리 연산
탐색 과정
해당 타겟 값이 나올떄 까지 타겟 값 보다 크면 오른쪽 서브 트리로, 타겟 값 보다 작으면 왼쪽 서브트리로 내려가며 찾게 됩니다.
시간 복잡도는 O(logN)이며 균형적이지 않을 경우 최대 O(n)이 걸릴 수 있습니다. 삽입과 삭제 또한 균형이 잡혀있지 않을 경우
탐색하는 시간이 많아져 O(n)이 걸릴 수 있습니다.
삽입 과정
새로우 노드를 삽입할 때 들어갈 자리가 비어있으면 그대로 값을 대입하면 되지만,
비어 있지 않을 경우에는 해당 자리의 노드 값과 비교하여 위치를 정해야합니다.
해당 자리의 노드가 삽입할 노드 보다 작다면, 왼쪽 오른쪽 자식 트리로 이동하면 됩니다. 그렇지 않고
해당 자리의 노드가 삽입할 노드 보다 크다면, 오른쪽 자식 트리로 이동하면 됩니다.
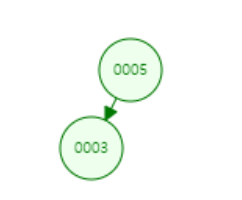
다음과 같은 트리가 있을 때 값이 4인 노드를 삽입하게 된다면, 어떻게 될까요? 원래 같으면 값이 3인 노드 자리에
들어가야 하지만, 해당 자리가 비어 있지 않으므로, 아래와 같이 3인 노드와 비교하여 오른쪽 자식 트리로 위치하게
됩니다.

위와 같은 삽입 연산을 수행할 때는 삽입할 위치를 탐색하는데 필요한 시간인 트리의 높이 O(logN)과 삽입하는 시간인 O(1)이 필요하므로 최종적으로 BST의 삽입의 연산 과정은 O(logN)이 됩니다.
삭제 과정
삭제 과정은 크게 3가지로 나뉩니다.
1. 리프 노드를 삭제하는 경우
제일 끝에 있는 노드 이므로 그냥 삭제하면 됩니다.
2. 자식노드가 하나인 노드를 삭제하는 경우
해당 자식 노드를 삭제할 노드의 위치로 끌어 올리면 됩니다.
3. 자식노드가 두개인 노드를 삭제하는 경우
왼쪽 서브트리의 MAX값과 오른쪽 서브트리의 MIN 값 중 하나를 삭제할 노드의 위치로 끌어올립니다.
3번 같은 경우 예를 들자면
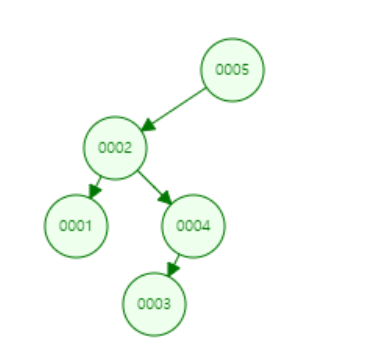
위와 같은 트리가 있을 때 2번 노드를 삭제하게 된다면, 왼쪽 서브트리의 최댓값인 1과 오른쪽 서브트리의 최솟값인 3중에 하나가 2번 노드에 위치하게 되고 2번 노드가 삭제되게 되는 것입니다.

최종적인 그림은 다음과 같게 됩니다.
삭제 과정또한 삽입과정과 마찬가지로 O(logN)의 시간복잡도를 지닙니다.
이상으로 이진 탐색 트리에 대해 살펴보았습니다.
글 읽어주셔서 감사합니다.
참고 자료
이진 탐색 트리 (Binary Search Tree)
BST 의 특징, 연산 시간 복잡도 알아보기
velog.io
https://saltyzun.tistory.com/24
[자료구조] BST(Binary Search Tree) 이진 탐색 트리 - CS면접 대비
이번 글에서는 탐색, 삽입, 삭제 연산에서 탁월한 성능을 보이는 BST(Binary Search Tree)에 관한 내용을 정리해보고자 한다. 1부터 100까지의 수 중 임의의 수 하나를 맞히는 게임을 한다고 가정해보자.
saltyzun.tistory.com
https://withhamit.tistory.com/282
트리 순회(전위 순회, 중위 순회, 후위 순회)
트리를 배우면 같이 배우게 되는 개념 중 하나죠. 트리 순회에 대해 알아보겠습니다. 트리 순회에는 전위 순회(preorder), 중위 순회(inorder), 후위 순회(postorder) 가 있습니다. 텍스트 추가 [그림 1]은
withhamit.tistory.com
'CS > 자료구조' 카테고리의 다른 글
| 레드 블랙 트리(Red-Black Tree) (0) | 2023.04.21 |
|---|---|
| Array와 List의 차이는? (0) | 2023.03.24 |
| Heap(힙)에 대하여 (0) | 2023.03.05 |
| HashTable이란? (0) | 2023.02.13 |
| B-트리 (B-tree)란? (0) | 2023.02.13 |